Bland-Altman Analysis

2つの測定方法の一致を評価

2種類の測定方法を同一の被験者40名に実施した結果を記録したサンプルデータを例に、ブランド-アルトマン分析の方法をご紹介します。Aが従来の測定方法、Bが新しく導入を検討している測定方法です。新しい測定方法Bは、従来よりも測定時間が短いため、導入することで測定時間の短縮効果が見込めます。従来の測定方法Aとの一致性が高ければ、測定方法Bでも測定方法Aと同等の結果が得られることを意味しますので、ブランド-アルトマン分析で2つの測定方法の一致性を確認してみます。

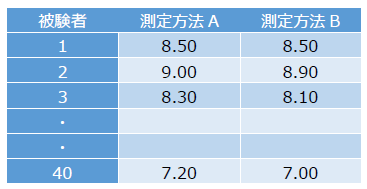
この分析では、Y軸に2つの測定方法の差、X軸に2つの測定方法の平均値を示した、ブランド-アルトマンプロットと呼ばれるグラフを作成します。グラフの参照線（破線）は、2つの測定方法の差の平均と誤差の許容範囲（limits of agreement；LOA）を示しています。2つの測定方法の差が誤差範囲内（LOA）であれば、2つの測定方法は同等である（一致性がある）と解釈することができます。

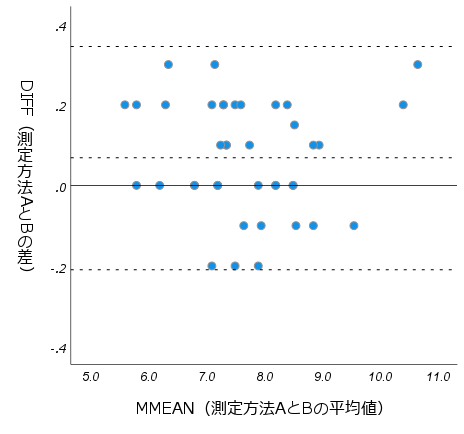
測定値に含まれている誤差に、系統誤差が存在せず偶然誤差のみであれば、誤差の大きさや範囲を推定することができます。そこで、ブランド-アルトマンプロットから、視覚的に系統誤差の有無を確認します。

偶然誤差と系統誤差

測定値には誤差が含まれており、「真の値＋誤差＝測定値」です。誤差は、偶然誤差（random error）と系統誤差（systematic error）の2つに大別されます。

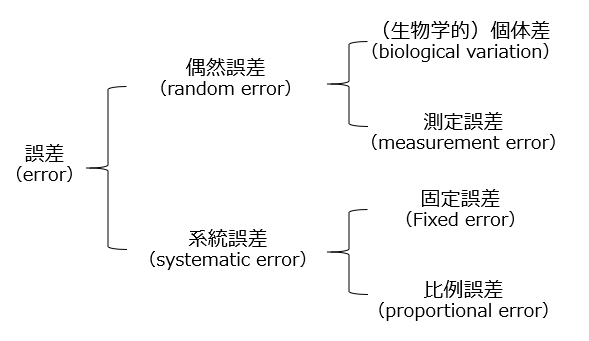
偶然誤差は、真の値に対してランダムに生じる誤差で、コントロールできない原因によって偶然に起きる誤差です。この例では、サンプリングした被験者の個体差や測定誤差などが偶然誤差と考えられます。 ブランド-アルトマン分析では、被験者ごとに2つの測定方法の差分をとることで被験者の個体差の影響を取り除いています。測定誤差は、真の値に対してランダムに生じるため、測定を繰り返すことで、誤差平均が0に近づき、この影響を小さくすることができます。 系統誤差は、真の値に対して一定の偏った傾向を持つ誤差のことで、コントロールできる原因（測定器の不備や測定者のクセなど）によって生じる誤差です。「偏り」または「バイアス（bias）」とも呼ばれます。

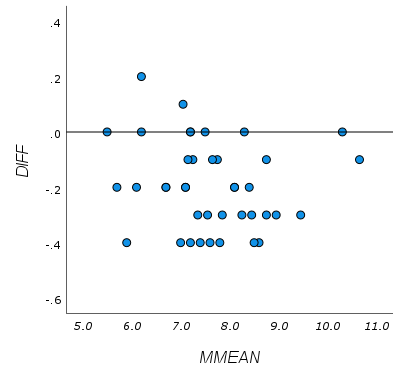
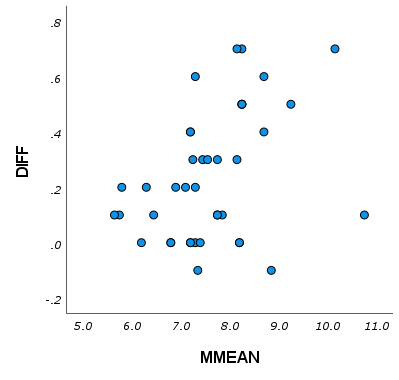
系統誤差は、測定を繰り返しても一定の傾向を持った偏りが生じ、その大きさを推定することは難しいため、系統誤差の有無を確認することは重要です。系統誤差はコントロールできる原因によって生じるため、その原因が分かれば取り除くことは可能です。 系統誤差は、さらに固定誤差（Fixed error）と比例誤差（proportional error）に分類されます。固定誤差は、真の値に関わらず、特定の方向へ一定の偏りを持つ誤差です。たとえば、測定方法Aよりも測定方法Bの方が小さく測定されてしまう場合などです。比例誤差は、真の値に比例して特定の方向に生じる誤差です。たとえば、測定値が大きくなるにつれ、誤差も大きくなる場合などです。 このような系統誤差が存在するかどうかを、ブランド-アルトマンプロットで視覚的に確認することができます。

偶然誤差のみの場合

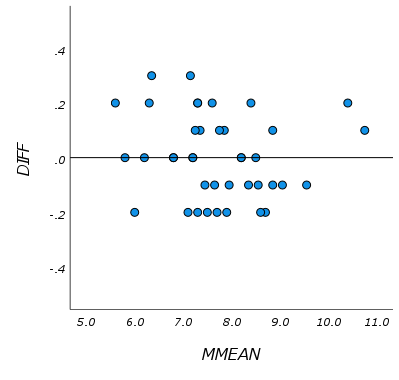
固定誤差が存在する場合

比例誤差が存在する場合

プロットによる一致性の評価

偶然誤差はランダムに生じる誤差であり正規分布に従う性質がありますので、この性質を利用して2つの測定方法の誤差の許容範囲（limits of agreement；LOA）を求めます。LOAは、「差の平均値±1.96×差の標準偏差」で計算され、2つの測定値の差が誤差として許容される範囲を表しています。誤差が正規分布に従う場合、95％がこの範囲に含まれますので、2つの測定値の差がこの範囲内であれば、2つの測定方法は同等である（一致性がある）と解釈することができます。

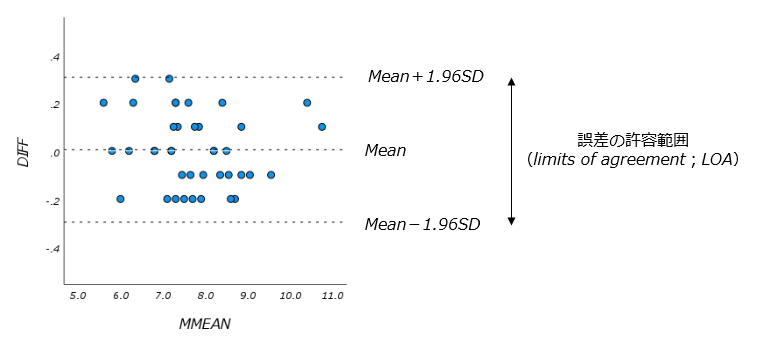
※上記のように、2つの測定方法の差の平均値と標準偏差（SD）を用いて誤差の許容範囲を示していますが、2つの測定方法の差の平均値と標準誤差（SE）を用いて誤差の推定精度についても確認しておくとよいでしょう。

ソフトウェア

SPSSでは、v30からBaseの機能でBland-Altmanプロット専用のメニューに対応しました。v29以前では、差と平均を計算し、散布図を作成してプロットを手動で作成可能です。Rでは、blandrパッケージなどを利用して、簡単にBland-Altman分析を実行できます。このパッケージはプロット作成を自動化し、CI（信頼区間）などの追加情報も提供します。Pythonでは、matplotlibやseabornなどのライブラリを使ってプロットを作成できます。statsmodelsなどを用いれば統計的な計算もサポートされます。