Mixed model

固定因子と変量因子を含むモデル

固定因子と変量因子は、統計モデル、特に混合モデルで重要な役割を果たす2つの因子です。このモデルは、個体差やグループ差を考慮した回帰モデルとしてよく使われます。混合効果モデルとも呼ばれます。

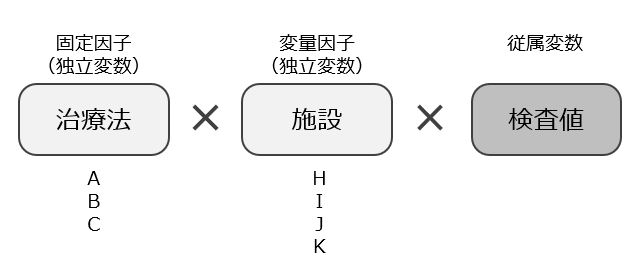
固定因子（Fixed Effects）とは、モデル内で一定の水準を持ち、その効果が全体にわたって一貫していると考えられる因子です。これは、研究対象の母集団全体に適用される推定値を表すもので、例えば、性別、治療群、教育レベルなどが該当します。固定因子は、データセット内でその全ての水準について推定が行われ、その影響が他のデータセットにも一般化されることが期待されます。

変量因子（Random Effects）とは、特定のグループやサブセットに関連する効果をモデル化するために使用され、データセット全体ではなく、一部のサンプルやグループに対して異なる影響を持つと仮定されます。変量因子の典型的な例は、学校や企業などのクラスターで、各クラスター内で個々の違いを捉えるために使用されます。変量因子は、グループごとの違いを考慮することで、モデル全体の精度を向上させる役割を果たします。

混合効果モデルは、これらの固定因子と変量因子を組み合わせたもので、個々のデータポイントに対して全体的なトレンド（固定効果）とグループごとの変動（変量効果）を同時に評価できます。これにより、複雑なデータ構造や階層的データに対して、より正確な分析が可能となります。

分散分析との違い

分散分析（ANOVA）は、データが独立している場合や、グループ間の効果を比較する際に非常にシンプルで効果的です。結果の解釈が容易で研究者が直感的に理解しやすいメリットがあります。ただし、データに階層構造がある場合には対応できず、固定因子しか扱えないため、個体差やクラスター間の差異を捉えることができないという欠点があります。

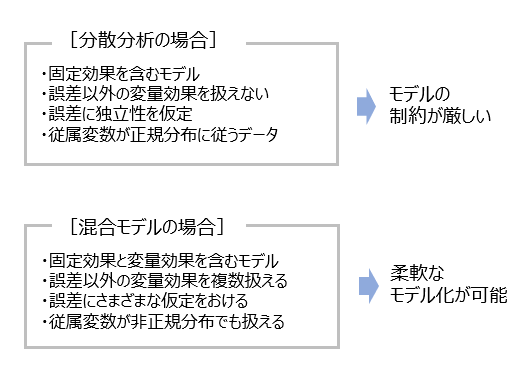
一方、混合モデル（Mixed Effects Model）は、固定因子と変量因子の両方を組み込んで分析できる柔軟な手法です。これにより、データ内の個体差やグループ差など、階層的な構造を捉えることが可能です。誤差が等分散性や独立性を持たない場合にも対応でき、例えば、時間が経過するにつれて誤差が相関するデータ（時系列データや繰り返し測定データ）や、クラスター内で誤差が相関するデータに対して、共分散構造を指定することができます。ANOVAでは、すべてのグループで完全なデータが必要ですが、混合モデルは欠測データにも柔軟に対応できるメリットもあります。ただし、分散分析に比べて計算が複雑で、解釈にも専門的な知識が必要となること、多くの因子や変量を含めすぎると、過剰適合のリスクがあるなどのデメリットもあります。

どちらの手法を推奨するかは、データの構造や研究の目的に依存します。単純なデザインで、固定因子だけを分析したい場合は、シンプルで解釈が容易な分散分析が適しています。階層構造や繰り返し測定、変量因子を考慮する必要がある場合は、混合モデルが推奨されます。混合モデルはより柔軟で、個々の違いやクラスター内の差異を捉えることができるため、精密な分析が可能です。

ソフトウェア

SPSSでは、Advanced Statisticsオプションが混合モデルに対応しています。GUI操作により、多様な共分散構造の指定が可能で、データの階層構造や繰り返し測定デザインを考慮した分析ができます。Rでは、lme4パッケージやnlmeパッケージが対応します。Pythonでは、代表的なライブラリとしてstatsmodelsが使用され、pandasやmatplotlibなど、他のPythonライブラリと組み合わせて使うことで、複雑なデータ操作や結果のビジュアライゼーションが柔軟に行えます。