Pearson’s chi-square test

質的変数の独立性の検定

Pearsonのカイ2乗検定は、2つの質的変数（カテゴリカル変数）が互いに独立しているかどうかを検定するために使用される統計手法です。この検定は、クロス集計表に基づいて観測されたデータと期待されるデータの差を評価します。

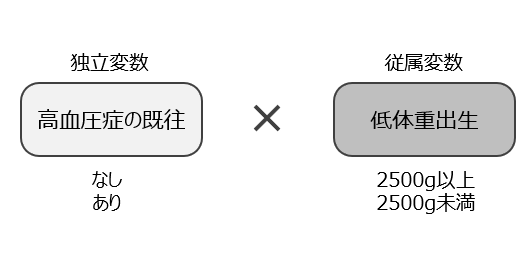
カイ2乗検定は、調査や実験のデータにおいて、2つの質的変数（例：性別と喫煙習慣、職業と居住地など）の間に独立性があるかどうかを調べることを目的とします。具体的には、観測されたカテゴリの頻度分布が、2つの変数が独立であるという仮定の下で予測される頻度分布とどの程度一致しているかを確認します。

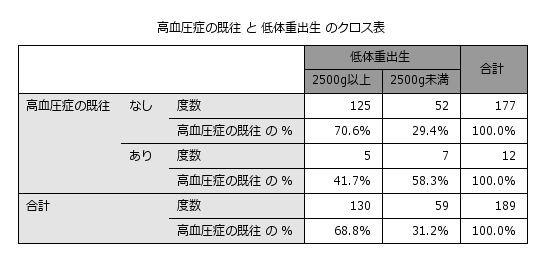
Pearsonのカイ2乗検定を用いると、クロス集計の結果が標本（サンプル）のみで言えることなのか、母集団全体に当てはまるのかを調べることができます。Pearsonのカイ二乗検定は、観測度数と期待度数の差に基づいて行われます。観測度数はクロス集計表に記載されている実際の人数（度数）であり、期待度数は2つの変数が関係がない（独立である）と仮定した場合に期待される人数です。観測度数と期待度数の差が小さいほど、2つの変数は独立している（関係がない）と解釈されます。

有意差の検定

検定結果は有意確率(p値)に基づいて解釈されます。p値が有意水準（通常0.05）未満の場合、観測度数と期待度数の差は偶然ではなく、2つの変数が独立していない（有意な関係性を認める）と結論付けます。p値が有意水準以上であれば、2つの変数は独立している（有意な関係性を認めない）と判断されます。

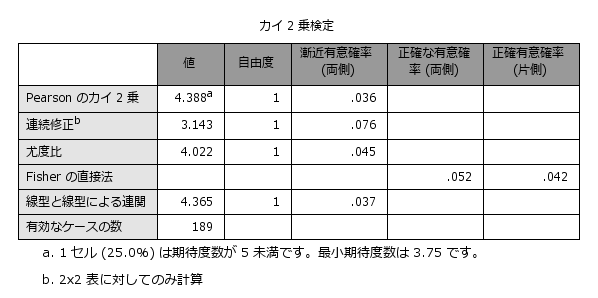
なお、カイ2乗検定は、期待度数が5未満のセルが多く含まれる場合、結果の信頼性が低くなる傾向があります。具体的には、期待度数が5未満のセルがクロス集計表全体の20%以上を占めると、カイ2乗検定は正確な結果を提供できない可能性があります。このような場合には、Fisherの正確確率検定を適用する対応が推奨されます。

また、カイ2乗検定を含む仮説検定は、サンプルサイズの影響を受けるため大きいサンプルの場合は有意な結果を導きやすくなります。具体的な差の大きさを示す効果量やその信頼区間、実用的な%の違いに注目して実質的な差を読み取ることが重要です。

ソフトウェア

SPSSでは、BaseのみでPearsonのカイ2乗検定の実行が可能です。2×2のクロス集計表では自動的にFisherの正確確率検定が実行されますが、それ以上のサイズのクロス集計表でFisherの検定を行うには、Exact Testsオプションが必要です。Rでは、chisq.test()関数を使ってPearsonのカイ二乗検定を実行でき、Fisherの正確確率検定にはfisher.test()関数を使用します。Pythonでは、scipy.statsライブラリのchi2_contingency()関数やfisher_exact()関数を使用します。