Two-way ANOVA

独立した2要因の平均値の比較

分散分析（Analysis of variance, ANOVA）は、対応のないグループ間の平均値の差を検定するための分析手法で、質的独立変数（因子/要因）によって量的従属変数の平均値を比較します。2元配置分散分析 Two-way ANOVA は、対応のない要因を2つ含む分散分析です。例えば、治療法による検査値について性別による差異が認められるかを分析したい場合、要因は「治療法」と「性別」の2つになります。

1元配置分散分析は1要因の効果（主効果）しか分析できませんが、2元配置分散分析では2つの要因の組み合わせによる効果（交互作用）を分析することができます。交互作用がない場合は、それぞれの要因（治療法、性別）の主効果を検討すればよいですが、交互作用がある場合は、それぞれの要因の主効果だけでは説明できない、組み合わせ特有の効果があることを意味するので、要因を組み合わせた検討が必要になります。

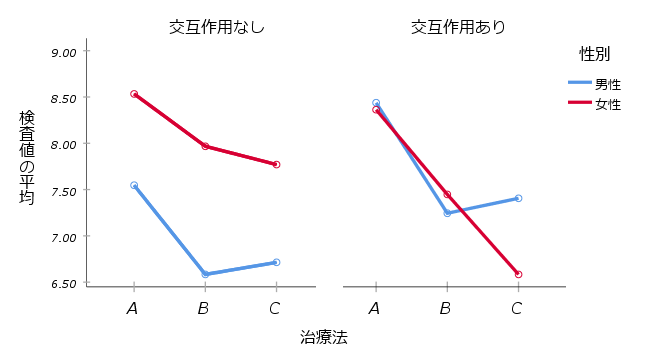
交互作用（治療法*性別）に有意差が認められた場合は、具体的にどの組み合わせの水準間に差があるかを調べる必要があります。治療法の各水準において男女差を調べる（または、性別ごとに治療法の差を調べる）この検定は、単純主効果の検定と呼ばれます。

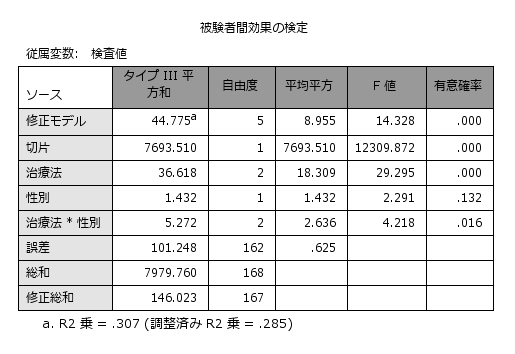
2元配置分散分析も1元配置分散分析と同じように「正規性」と「等分散性」の仮定が必要ですが、仮定を満たさない場合でも、代替としてノンパラメトリック検定やウェルチ検定を使用することはできません。

ソフトウェア

SPSSでは、基本機能のBaseのみで対応しており、v28以降では単純主効果の検定もGUIで実行できます。ただし、対応のある要因を含む2元配置のモデルを実行するには、Advanced Statisticsオプションが必要です。Rでは、aov()関数を使用してモデルを作成し、summary()関数で結果を表示します。Pythonでは、statsmodelsライブラリを使用します。ols()関数でモデルを作成し、anova_lm()関数でANOVAテーブルを表示します。