Multiple Comparison Procedure

複数の比較による誤判定を抑制

多重比較法（Multiple Comparison Procedure）は、水準間の平均値の差を比較する検定手法です。多重比較法を用いると、3水準以上の比較において、どの水準間に差があるかを調べることができます。水準間の平均値の差を調べる方法として、t検定を利用することも考えられますが、t検定で2群ごとの比較を単純に繰り返してしまうと、検定の多重性の問題が起こります。

例えば、3種類の治療法（A、B、C）についてそれぞれ比較する場合、検定を3回繰り返すことになりますが、1回あたり0.05（5%）の有意水準で検定を行っているため、検定を繰り返すことにより最終的な有意水準が0.05（5%）よりも大きくなってしまいます。

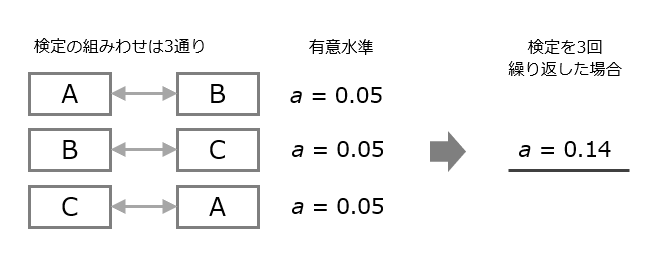
多重比較法は、このような問題を回避するために、全体の有意水準をあらかじめ設定している有意水準になるよう調整を行う検定方法です。多数の手法が考案されているので、目的に合わせて適切な手法を選択します。

正規性と等分散性を仮定する多重比較法では、テューキー（Tukey’s honestly significant difference test）の方法がよく利用されており、HSD検定とも呼ばれます。その他、分散分析を先行させた場合に結果が一致するシェフェ（Scheffe）の方法や、1つの対照群と複数の処置群を比較するダネット（Dunnett）の方法などもよく利用されます。

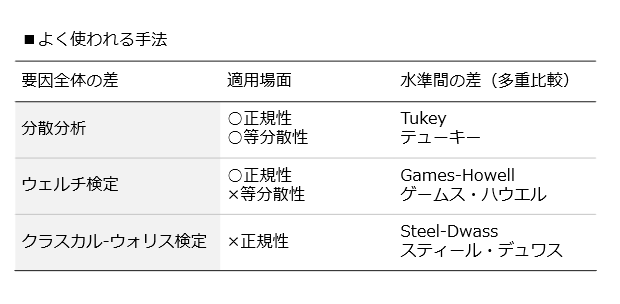
正規性を仮定するが等分散性を仮定しない多重比較法では、ゲームス・ハウエル（Games-Howell）の方法があり、ウェルチ検定によって要因の差を調べた場合の水準間の検定としてよく用いられます。

多重比較法の中でも計算が容易で有名な手法がボンフェローニ（Bonferroni）の方法で、検定の回数に基づいて有意水準または有意確率を調整します。例えば、治療法A、B、Cをそれぞれ比較する場合、検定は全部で3回行われるので、有意確率をそれぞれ3倍（または有意水準を1/3）にして判定します。

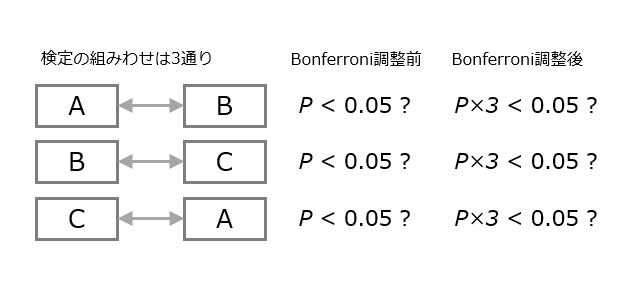
ボンフェローニの調整は、手計算で簡単にでき、あらゆる検定に適用できる利便性を持ちますが、一方で、検定の回数が多い場合は保守的になる欠点があります。そこで、より効率的な調整方法として、ホルム法（Holm’s step-down procedure）の方法などが提案されています。

多重比較は、伝統的・慣習的に分散分析で全体の差を調べた後の下位検定として実行されることが多いですが、研究の目的が群間の個別差の検出であるならば、分散分析を行わずに直接多重比較法を適用するアプローチもあります。

ソフトウェア

SPSSでは、基本機能のBaseのみで多重比較の手法に対応します。Rでは、multcompやstatsなどのパッケージを使用します。Pythonでは、statsmodelsやscipyなどのライブラリを使用可能です。