Correlation coefficient

2変数の線形の関係性の指標

相関係数は、2つのスケール変数の関係性を調べるための2変量解析の手法です。相関関係は直線で要約されるものであり、線形相関とも呼ばれます。小文字のrで表記され、-1≦r≦1の範囲をとり、+は正の相関、‐は負の相関を意味し、絶対値が1に近いほど関係性が強いことを意味します。ただし、相関係数で曲線相関を調べることはできないため、外れ値の吟味の目的も含めて散布図によるグラフの評価が必要です。

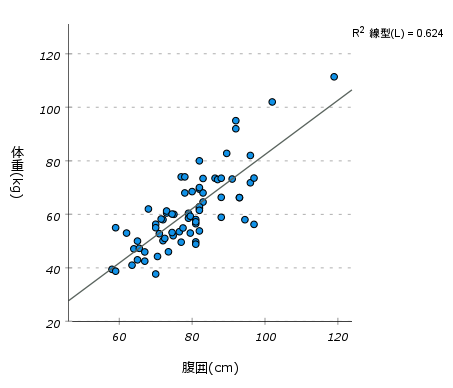
Pearsonの積率相関係数は、最も一般的に使われる相関係数で、2つの連続変数の間にどれだけ線形関係があるかを測定します。データが正規分布に従い、線形関係があることが前提です。Spearmanの順位相関係数は、データの順位（ランク）に基づいた相関を測定します。非線形関係や外れ値がある場合でも適用可能で、データが正規分布に従わない場合や、順序尺度のデータに適しています。Kendallの順位相関係数は、2つの変数間の順位の一致を測定し、特にデータが小規模な場合や、データに外れ値が含まれている場合に有効です。Spearmanの相関係数と似ていますが、計算方法が異なります。

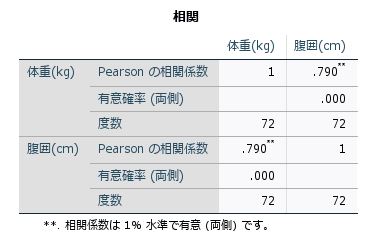
相関係数は、因果関係を示すものではないため、2つの変数が相関していても、片方が他方の原因であるとは限りません。また、相関係数は線形関係を測定するため、非線形の関係がある場合、正しい関係性が捉えられないことがあります。外れ値があると、Pearsonの相関係数が影響を受けるため、データの特性に応じてSpearmanやKendallの相関係数を使用することが推奨されます。

相関係数は、単純に2変数の関係性を示す指標ですので、背景として影響する変数（交絡/共変量）がある場合は偏相関係数を用いたり、重回帰分析などの多変量解析を必要とします。

ソフトウェア

SPSSでは基本機能のBaseのみで相関係数、有意確率、信頼区間を計算可能です。偏相関係数や回帰分析も基本機能として提供されます。Rではstatsパッケージがデフォルトで提供されており、基本的な相関係数の計算が可能です。Hmiscやpsychパッケージを使うと、p値やより詳細な情報も取得できます。Pythonではpandasやscipyが主要なライブラリとして使われています。