Structural Equation Modeling

変数間の複雑な関係性の分析

構造方程式モデリング（Structural Equation Modeling, SEM）は、直接観測されている変数（観測変数）の背後に直接観測されていない変数（構成概念/潜在変数）を仮定して、さまざまな要因の関係性を分析する手法です。 観測変数の背後にある因子を探索するタイプの因子分析（探索的因子分析）に対して、確認的因子分析とも呼ばれますが、構造方程式モデリングは重回帰分析や因子分析を下位概念として包括します。共分散構造分析（Covariance Structure Analysis,CSA）とも呼ばれる手法です。

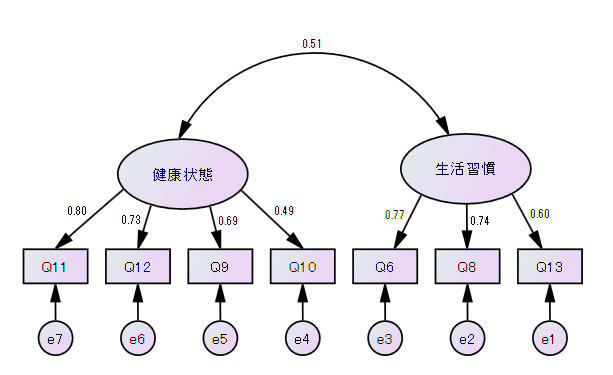
パス図は、構造方程式モデリング（SEM）のモデルを視覚的に表現したもので、変数間の因果関係を矢印で示します。パス図はSEMの複雑なモデルをわかりやすく表現し、関係性を視覚的に理解するために使用されます。

SEMは、複数の回帰分析、因子分析、パス解析などを統合したモデルであり、直接的な影響だけでなく、間接的な影響や潜在変数（測定できない理論的な概念）の関係性も評価できる点が特徴です。

モデルの適合度

適合度指標は、構造方程式モデリングのモデルがデータにどれだけ適合しているかを評価するための統計指標です。SEMは、複数の方程式を同時に扱うため、モデルの適合度を確認することが重要です。適合度指標にはいくつかの種類があり、モデルの良さを複数の観点から評価します。

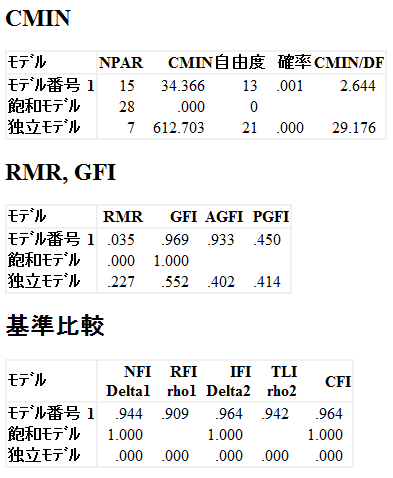
例えば、GFI（Goodness-of-Fit Index）とAGFI（Adjusted Goodness-of-Fit Index）は、モデルがデータにどれだけフィットしているかを直接的に評価する指標です。GFIは、データに対するモデルの適合度を0から1のスケールで表し、値が1に近いほど適合度が良好であることを示します。AGFIは、モデルの複雑さに基づいてGFIを調整した指標で、モデルが複雑になるとAGFIが低下するよう設計されています。両指標とも、値が0.90以上であればモデルの適合度が良好と判断されます。

これらの適合度指標はそれぞれ異なる視点からモデルの適合度を評価するため、1つの指標だけでなく、複数の指標を組み合わせて評価することが重要です。特にカイ二乗検定がサンプルサイズに敏感なため、GFI、CFI、RMSEA、SRMRなど他の指標を併用することで、モデルの全体的な適合度をバランスよく判断することが推奨されます。

なお、SEMは、潜在変数や複数の要因が絡む複雑な因果モデルを扱うための強力なツールですが、仮定に依存しやすく、サンプルサイズやモデルの複雑さによる制限があります。一方、LiNGAMと呼ばれる手法は、データから因果関係を推定することが可能な新しいアプローチであり、非正規分布を扱える点や因果構造の自動推定という点で、SEMの弱点を補完する手法として注目されています。

ソフトウェア

SPSSでは別製品のAmosがSEMに対応しています。SPSS Statisticsと独立しているため、Excel等をデータソースとして単独で使用可能です。Rではlavaanパッケージを使用し、semPlotでパスの強さや方向を直感的に示すパス図を作成します。Pythonではsemopyが適したライブラリであり、statsmodelsやPyMC3などと組み合わせて使用することが推奨されます。