Kaplan-Meier method

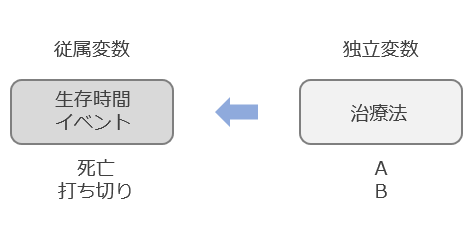
生存時間の比較

カプラン・マイヤー法の特長として、期間内にイベントが起きなかった例を「打ち切り」として分析に含めることができる点が挙げられます。例えば、手術から再発までの時間を分析する際に、途中で転院したり、治療を中断したケースは、少なくとも再発していないためイベントに該当しませんが、欠損値として分析から除外してしまうとバイアスがかかります。打ち切り例は、イベントが起きるまで（打ち切りになるまで）は生存率の計算に寄与し、打ち切り後はケースから除外される形で扱われます。

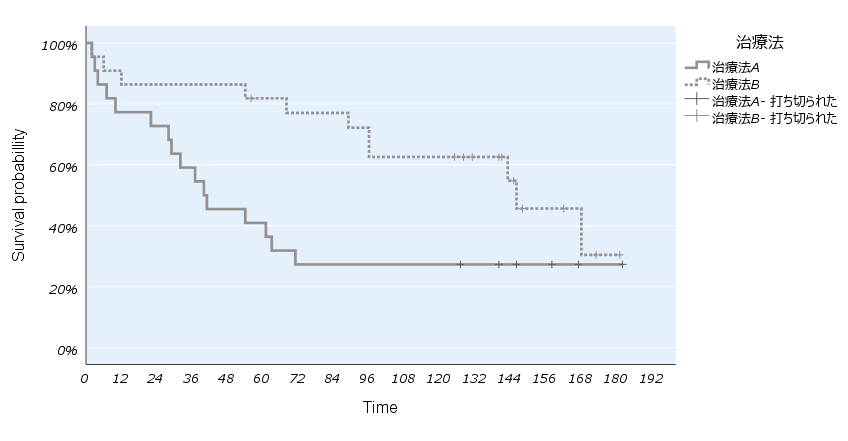
生存曲線は、横軸に時間、縦軸に生存率を示したグラフで、ある時点における生存率を確認したり、グループによる差を比較できます。この例では、2つの治療法による生存率の違いを視覚化しており、治療法B の方が、生存率が高いことが読み取れます。また、打ち切り例には縦線などの記号がプロットされますが、生存率が更新されず、グラフが水平に推移していることが分かります。

有意差の検定

生存時間は、打ち切りも含まれるため、代表値は平均値ではなく、中央値がよく利用されます。中央値は、50%が死亡し残りの50%が生存するちょうど半分の時間です。以下の例では、治療法Aの中央値が40か月、治療法Bの中央値が146か月で、治療法Bの方が治療効果が高いことが読み取れます。

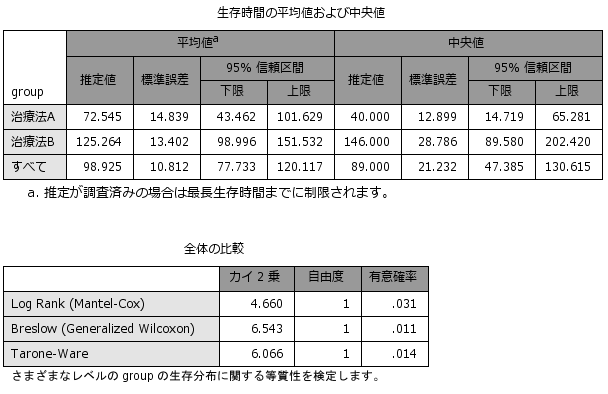
有意差が認められるかどうかを調べる場合、ログランク検定（Log Rank test）がよく用いられています。IBM SPSS Statisticsでは、そのほかに、一般化ウィルコクソン検定（Generalized Wilcoxon test）、タローン・ウェア検定（Tarone-Ware test）の実行が可能です。

カプラン・マイヤー法は、独立変数（要因）を1つしか使えませんので、患者の年齢・性別・体重などのその他の要因(交絡/共変量)の影響を考慮していません。つまり、単変量の解析に該当します。Cox回帰分析(比例ハザードモデル)を用いると、複数の共変量を用いた多変量解析に拡張することができ、患者の背景因子を制御した影響の大きさを調べることができます。

ソフトウェア

SPSSでは、Advanced Statisticsオプションが生存時間分析に対応しています。分析メニュー内に「生存分析」が追加され、Kaplan-MeierやCox回帰分析を実行可能です。Rでは、survivalパッケージを使用してKaplan-Meier法を実行します。このパッケージは生存曲線の作成や生存時間の推定をサポートしており、詳細な解析も可能です。ggsurvplotを使えば、美しいグラフも作成できます。Pythonでは、lifelinesやscikit-survivalなどのライブラリを使用してKaplan-Meier法を実行します。これらのライブラリは、生存分析に特化しており、Kaplan-Meier曲線の作成や統計的解析を効率的に行えます。