Paired-samples t-test

対応のある2群の平均値の比較

t検定（t-test）は、検定統計量t値を利用する検定手法の総称で、2つのグループ間の平均値の差の検定を行う場合によく利用されます。対応のあるサンプルのt検定（Paired-samples t-test）は、比較するサンプルに対応がある場合のt検定です。前後の比較など、同じ対象について2つの測定値をペアにして比較する際に使用されます。

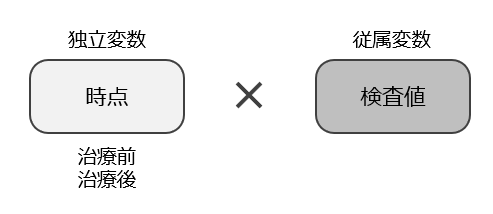
例えば、治療の効果を調べることを目的として「治療前」と「治療後」の2つのグループの検査値を比較するためにt検定を行います。このとき、治療前後の検査値の変化をみるために、同じ被験者について治療前と治療後の2時点で検査値を測定します。「治療前」と「治療後」のグループのサンプルには対応があるため、対応のあるサンプルのt検定を用います。

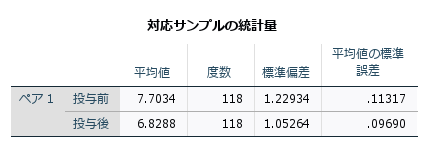
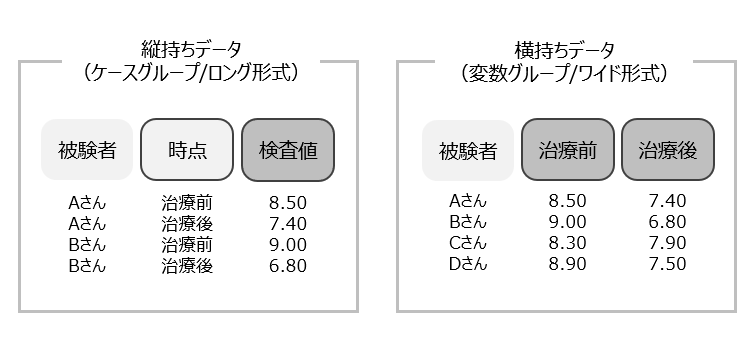
対応のあるサンプルのt検定を実行する場合、データセットの持ち方は横持ち（変数グループ/ワイド形式）である必要があります。データの持ち方が縦持ち（ケースグループ/ロング形式）になっている場合は、データの再入力または再構成を行う必要があります。

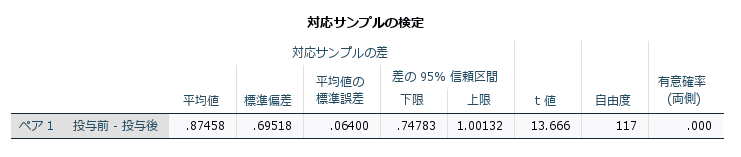
独立したサンプルのt検定と同様に、有意差が認められた場合は、母集団において2つのグループ間の平均値の差が0ではないことを意味するのみであり、どの程度の差があるかまでは分かりません。そこで、差の95%信頼区間を用いて、2つのグループの差の大きさの推定や効果量による評価も重要です。

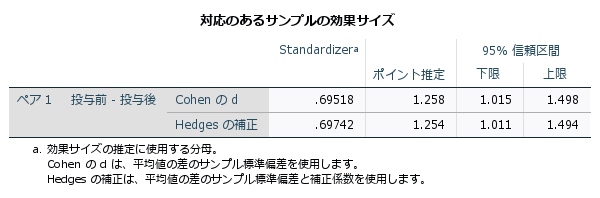
対応のあるサンプルのt検定は、2つのグループの量的従属変数の差が正規分布にしたがう「正規性」の仮定を持ち、この仮定を大きく逸脱する場合はノンパラメトリック検定として、ウィルコクソン符号付順位検定（Wilcoxon signed rank test）を適用する方法があります。

ソフトウェア

SPSSでは、基本機能のBaseのみで実行可能です。Rでは、t.test()関数を使って対応のあるt検定を実行します。Pythonでは、scipyライブラリのttest_rel()関数を使用することができます。