Repeated Measures ANOVA

繰り返し測定した値の平均の比較

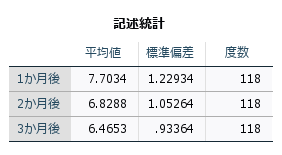
反復測定分散分析は、同じ対象に対して複数の時点や条件で繰り返し測定したデータの平均値の違いを評価する手法です。慣習的に、2時点の場合は対応のあるt検定が適用され、3時点以上の場合は反復測定分散分析（や混合モデル）が適用されます。この分析では、調整変数として年齢や体重などの共変量を使用することも可能です。

反復測定分散分析には、球面性(球形性)と呼ばれる仮定があります。球面性を調べるためにMauchly(モークリー)の球面性検定を使用し、球面性を満たさない場合はGreenhouse-Geisser（グリーンハウス・ガイザー）などの補正P値を使用する方法があります。または、共分散構造として球面性以外を指定することができる混合効果モデルを使用します。

なお、球面性は反復測定の水準が3つ以上の場合の仮定です。前後比較など2水準の場合は、対応のあるt検定の場合と同じく球面性は問題になりません。

反復測定分散分析では、介入と非介入を意味する群間要因を組み合わせた2元配置のモデルがよく用いられます。この場合、介入効果（群間効果）と時間効果（反復効果）の両方を評価することができます。また、介入効果と時間効果の交互作用（介入×時間効果）を評価することも可能です。

反復測定分散分析を実行する場合、データセットの持ち方は横持ち（変数グループ/ワイド形式）である必要があります。データの持ち方が縦持ち（ケースグループ/ロング形式）になっている場合は、データの再入力または再構成を行う必要があります。

ソフトウェア

SPSSでは、Advanced Statisticsオプションが反復測定の分析に対応します。Rでは、簡単に実行できるezやafex、混合効果モデルを扱うnlmeやlme4パッケージがあり、目的やデータの複雑さに応じて使い分けることができます。Pythonでは、statsmodelsやpingouinライブラリを利用する方法があります。